• Guo Wu Guan
  過五關

• Introduction
• Layout
• Valid Triplets
• Play
• Winning and Losing
• Variations
• Other Websites

Introduction

This is a solitaire game using a standard set of 32 Chinese dominoes. The name means "Passing Five Levels", which refers to the phrase "Pass five levels and cut six generals" from the novel "Riding a Thousand Miles" by Guan Yu from the Three Kingdoms period.

The set has 21 different tiles (all possible pairs of numbers from 1 to 6) plus duplicates of 11 of them. The duplicated tiles are the six doubles plus the [3:1], [6:5], [6:4], [6:1] and [5:1].

This page is based on a contribution from Dmytro Polovinkin with help from Min Fanxin (闵凡信).

Layout

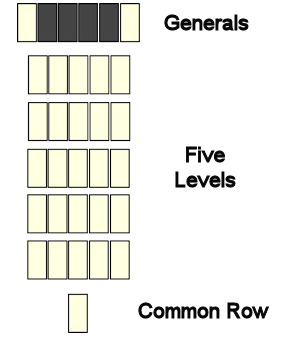
The 32 tiles are shuffled and the laid out as follows.

• At the top is a row of six tiles representing the generals. Only the left and right hand general tiles are face up: the middle four begin face down.
• Below the generals are five rows of five face up tiles: these are the five levels that must be 'passed'.
• At the bottom is a 'common row' (guang gong: 關公) which at the start has just one tile. During the game tiles are added to the left of this common row and taken from the right.

The initial arrangement is like this (tiles shown with dark colour are face down)):

Valid Triplets

The play of the game is based on moving valid triplets, which are particular sets of three tiles

There are nine types of valid triplet, based on the combinations of six numbers on the six tile-ends: it does not matter how the numbers are distributed across the three tiles. The first three are triplets that include three equal ends.

1. Five points. Exactly three equal ends, and the pips on the other three ends add up to 5. Example [3:3][3:1][2:2]. Note that there cannot be more than three equal ends, so for example [3:3][3:1][3:1] and [1:1][1:1][2:2] are not valid triplets.
2. Full fourteen. Exactly three equal ends, and the pips on the other three ends add up to 14 or more. Example [1:6][1:6][1:4]. Note that as with 'five points' there cannot be more than three equal ends, so triplets such as [5:5][6:5][5:4] are not valid.
3. Split. Two sets of three equal ends. Example [1:1][1:6][6:6].

The next two require four or five equal ends.

4. Coincidence. Four equal ends, and the total of the pips on the other two ends also equals the same number. Example [5:5][5:3][5:2], having four fives coinciding with 3+2 which is also five.
5. Five sons. Five equal ends. Example [1:1][1:1][1:3].

Each of the last four requires a spread of single numbers or pairs of numbers.

6. All different (or Full dragon). All ends are different - one of each number 123456. Example [1:3][2:6][4:5].
7. Small dragon. Two of each of the small numbers 1, 2 and 3. Example [1:3][1:3][2:2].
8. Big dragon. Two of each of the large numbers 4, 5 and 6. Example [4:4][6:5][6:5].
9. 2-3-Kao. Two 2's, two 3's and two 6's. There are only two ways to make this: [2:2][3:3][6:6] or [2:3][2:6][3:6].

Play

The play consists of three phases, which are repeated until the game is either won or lost.

1. Removing triplets from levels

For each level, starting from the top level and working downwards, if the level contains three adjacent tiles that from a valid triplet, they are removed from the level and added to the left end of the common row. The leftmost and rightmost tiles in a level are considered to be adjacent, so a player may choose to take two tiles from the left of a level and one from the right or two from the right of a level and one from the left if they form a valid triplet. If three tiles are taken from the interior of a level the remaining tiles are slid together to close the gap.

2. Passing levels

For each level, starting again from the top level and working downwards, if the level contains exactly two tiles that form a valid triplet together with one of the exposed generals, these three tiles can be moved to the left end of the bottom row. In this case the level is passed, reducing the number of levels in the game by one, and the general is cut, reducing the number of generals by one. If a level contains only one tile which forms a valid triplet with the two exposed generals, the three tiles may be moved to the left end of the common row, passing the level and cutting both the generals. Whenever a general is cut the adjacent general which is now at the end of the row is turned face up, so that there are always two exposed generals (until only one general remains).

3. Replenishing levels

For each level, starting from the bottom level and working upwards, take the right hand tile of the common row and add it to the right hand end of the level. Note that a level may be empty but still in the game: this happens if its last three tiles were removed as a triplet in step 1. In this case a tile from the common row must be placed in it. In the unusual case where there are fewer tiles in the common row than remaining levels then it may not be possible to add a tile to the top level(s).

Winning and Losing

The object of the game is to pass all five levels and cut all six generals. To achieve this, there must be exactly one occasion in the game when a level containing a single tile is used to cut two generals at once. When all the levels are passed and all the generals cut the player wins the game.

The game is lost if the common row is empty and there is no valid triplet of adjacent tiles in any of the remaining levels.

Variations

There is an more lenient version of the game in which the tiles removed from a level in step 1 of the play do not need to be adjacent. Any set of three tiles in a level that form a valid triplet can be moved to the left end of the common row.

Versions with no Generals

In his book, Chinese Games With Dice And Dominoes (1895) Stewart Culin describes a very similar game O-Koan (equivalent to Chinese Wu Guan - 5 gateways), presenting it as a method of divination. Five levels of four pieces are dealt, leaving a common row of 12 pieces, which are stored face down at the top of the layout. The player goes through the levels from bottom to top removing valid triplets, which can either consist of three adjacent pieces or of two pieces from one end of a row with one from the other end as above. The removed triplets are added to one end of the common row and when the player has been through all the levels, pieces are taken from the other end of the common row and one is added to the right hand end of each level that is not empty. The process is repeated until either all the levels are empty (success) or the common row is empty and no more valid triplets can be removed from the remaining levels (failure).

Another variant 通五关 (TongWuGuan) is similar to O-Koan except that it begins with 6 pieces in each level and just 2 pieces in the common row.

Version with one General

Another variant, created by 杨钧陶 (Yang Juntao) and improved by MinFanXin is called "七擒孟获" (Seven captures of Meng Huo). This has a single general [1:2] - called Meng Huo, seven levels with 3 pieces each and a common row of 10 pieces. The play is the same as in Guo Wu Gan.

Whenever the [1:2] is captured it is added to the common row, where it remains until reaches the other end of the row and is released during the level replenishment phase. At this point it is not added to an ordinary level but is moved back into the general's position by itself at the top of the layout. In order to clear a level it must have exactly two pieces that form a triplet with the general (empty levels that have not been cleared in this way are given a piece during the replenishment phase). Therefore the general must be captured 7 times to clear all rows and win the game.

Other Websites

Here is a blog showing the play of an example game. (Archive copy. The layout is shown with all six generals face up but in an actual game only the generals at each end of the row would be exposed at any time).

There is a description of the game in Chinese Wikipedia.