Dominoes-Matrix

Contributed by Mal Jones

Dominoes-Matrix is a game for two or more players depending on the size of the domino set used. Players aim to gain points by creating “cells” (empty spaces surrounded by dominoes) and also scoring with specific “double figure combinations” on the playing surface. The player with the most points scored when the last piece is played wins. A standard set of dominoes (double 6) is used in this illustration but larger sets such as double-9, double-12 or double-15 can be used.  There are three game options based upon how the tiles containing blanks are played.

Setting up the game and the basics of play:

After shuffling the stock with tiles face down, each player draws two tiles.

• Each player starts their first turn of play with two tiles.
• In each turn a player may ‘put down’ one or two tiles, adding them to the layout on the playing surface.
• After putting down one or two tiles, a player draws two new tiles from the stock. [When the stock is empty, play continues without drawing.]
• A player may ‘pass’ in a turn without putting down any tiles, for example if unable to place a tile or if they choose not to do so for tactical reasons. However, when a player passes, all opponents of that player receive a bonus score of one point. A player who passes may in that turn exchange any number of tiles from their hand with others from the stock but this is not compulsory.  The tiles to be exchanged are set aside temporarily, an equal number of new tiles are drawn from the stock, and then the rejected tiles are then shuffled together along with the remaining stock.

Joining tiles:

When putting down tiles, the following rules are followed.

• Tiles may be joined at right angles either at an end or at a side of a tile, or tiles may be joined in parallel: long-side against long-side, with or without an offset. Tiles cannot be joined end to end - see illustration.
• Tiles are matched using matador rules. A number is not joined to an equal number. Instead for a double six set, joined numbers have to make a total of 7. For a double nine set joined numbers have to add up to 10, for a double twelve set they have to add up to 13, and so on.
• There are three versions of the game, corresponding to three different ways of playing blanks.
  • Game Option 1: Blanks can be used as “wild cards” where they are without number in and may join with any tiles regardless of numeral including other blanks.
  • Game Option 2: Blanks count as zero and can be joined only to other blanks, not to any other number.
  • Game Option 3: This more complex option is explained in the addendum. The main body of this text deals with Game Options 1 and 2.
• Play continues until all players have placed their tiles; some players may therefore finish before others.

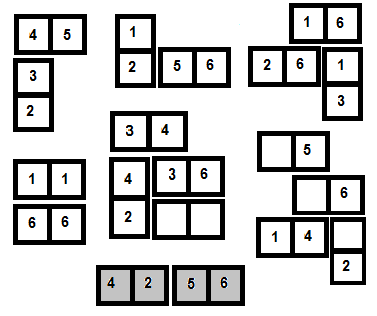Throughout this text, the diagrams illustrate play with a double six set. Illustration 1 shows examples of individual and multiple tile arrangements, with all joins using a sum of seven. The use of ‘blanks’ as “wild cards” using Game Option 1 is also shown. An incorrect method of placing tiles end to end (shaded tiles) is shown for reference only.

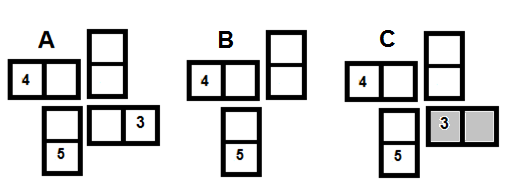Illustration 2 shows Game Option 2: Blanks may only be joined to each other. Some examples of this feature are shown in graphics A and B. Note that the shaded [3:0] tile in graphic C would be illegal as played here.

Creating and scoring with ‘cells’

The main aim of the game is to create enclosed spaces upon the playing surface; each ‘cell’ has the area of one half of a domino tile. One point is scored for each cell created. The following illustration shows examples of cell creation.

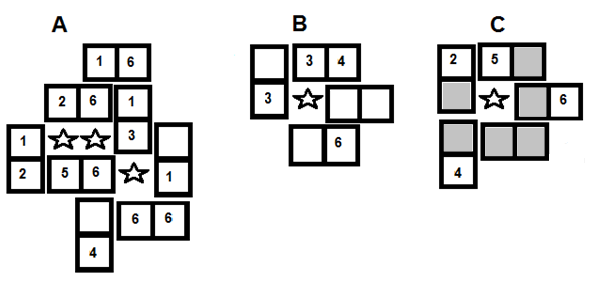
• Graphic A shows tactics using Game Option 1 and the creation of three cells - a double score and a single cell - marked with stars for clarity.
• Graphic B shows another example of using ‘blanks’ with Game Option 1. Their 'wild card' status enables more flexibility of play than with Game Option 2 and 3.
• Graphic C shows an example of ‘blanks’ (shaded for clarity) being used with Game Option 2, in which blanks may only connect to themselves.

Creating and scoring with "Double Figure Combinations"

Placing a tile so that both end numbers of the played tile create a sum of seven with at least one adjacent tile will score one point. There are two main ways of doing this: playing a doubles alongside a complementary double, such as [6:6] next to [1:1] or [3:3] next to [4:4], or playing tiles with different ends that adjoin two different tiles on the layout. Illustration 4 below shows the method using ‘doubles’.

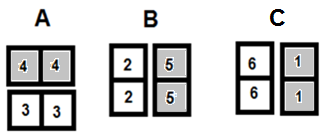
In each case playing the shaded tile scores 1 point. Illustration 5 below shows examples where the played tile is not a double - again playing the shaded tile scores a point.

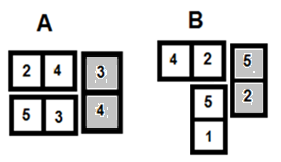
• Graphic A shows the tile [3:4] (shaded) completing a double figure combination when placed alongside the [2:4] and [5:3] tiles from a previous double figure score.
• Graphic B shows a double figure combination using a [5:2] tile (shaded).

Note: double figure scoring is made by the action of placing a single tile. Regardless of the number of connections made only one point is scored by doing so - see the [1:5] tile in the game scenario in illustration 8.

Double figure combinations and blank tiles

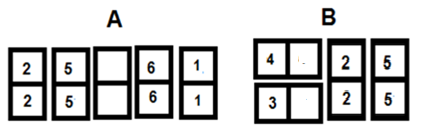
Illustration 6: The placing of a blank tile may not be used to score a double figure combination in either Game Option 1 or 2. However, a player may use blank tiles to set up further combinations when playing Game Option 1.

• In Graphic A the [6:6] tile being placed alongside the double blank allows a [6:6] / [1:1] combination.
• In Graphic B the [2:2] / [5:5] combination can placed alongside the existing 4: blank and 3: blank tiles.

Note: In Game Option 2 ‘blank’ tiles’ may not be used to create or set up double figure combinations. For Game Option 3 rules, see Addendum at end.

Maximising scoring from double figure combinations

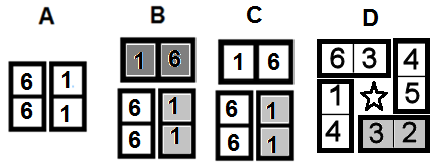
Illustration 7:

• Graphic A shows a [1:1] tile completing a double figure combination against the [6:6] tile scoring one (1) point.
• Graphic B shows that if the [6:6] had already been placed on the Matrix in a previous play by placing the [1:1] tile first (light shading) then followed by the [1:6] (darker shading) in the same turn two (2) points would be scored.
• Graphic C shows that if the [1:6] tile were placed against the [6:6] first, only one (1) point can be scored in the turn of play if the [1:1] tile is then placed against the [6:6] tile.
• Graphic D: by placing the [3:2] tile both a cell and double figure combination are scored, for two points.

Illustration 8 shows a game in progress under Option 1 rules:

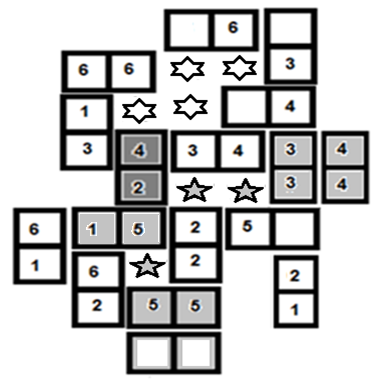
Illustration 9 shows a completed game using Option 1

The first tile put down was the shaded [1:3]. Player 1’s cells are shown with the five pointed stars and Player 2 has the six sided stars.

Addendum

In Game Option 3 the tiles with blanks are used as wild cards but their value is determined by the numeral that it is in contact with.

Connecting blank tiles to numbered tiles using Game Option 3

Illustration 10: For this illustration all blank tiles are shaded.

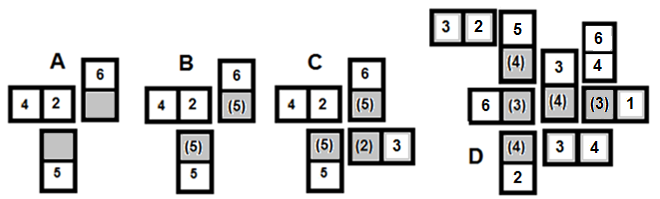
• Graphic A shows two blank tiles connected to the [4:2] tile; the numeric value of the [6: blank] and [5: blank] must now become 5 for a “double six domino set” as shown in graphic B with the number (5) in brackets.
• Graphic B and C show that any other blank connecting to this arrangement must obey the principles of making the sum of seven (7) therefore the [blank: 6] tile becomes a [5:6:] and the [blank: 5] becomes a [5:5]. The [blank: 3] becomes [2:3].
• Graphic D shows blank tiles connected and obeying the placing rule. Notice that it is possible to have duplication of numbers in such circumstances; see the [3:4] and [blank: 3] tile which has now become a [4:3] itself.

Connecting blank tiles to other blanks with Game Option 3

Illustration 11: Connected blanks are zero as is the case with Game Option 2.

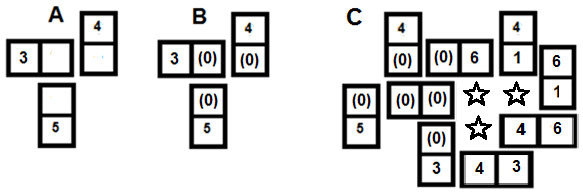
• Graphic A shows [blank: 3], [blank 4] and [blank: 5] tiles connected without being influenced by tiles with numerals; the blanks become zero as with Game Option 2.
• Graphic B and C show that any connected blanks would be valued as zero and only other blanks may be joined to them as is also the case with Game Option 2.

Creating Double Figure Combinations with ‘blanks’ in Game Option 3

Creating double figure combinations in Game Option 3 is possible if the value of the blank has already been determined by the placing of a numeral against it - see Graphic A, B and C of illustration 12.

However, Graphic D shows that it is not possible to make double figure combinations if the blanks are valued as zero as the only value the tile marked with an X can have is also zero.

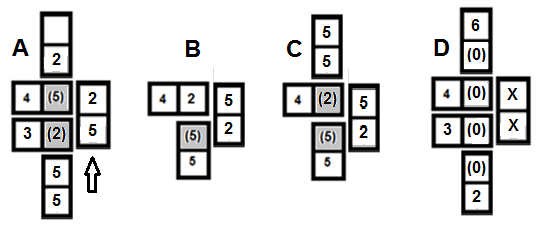
In graphics B and C, a double figure combination is scored if the [5:2] tile is placed last, against those already on display.

In graphic A, the double figure score with the [5:2] is only possible if the values of the two blanks have already been fixed as 5 and 2 (by the 2-tile above and the 5-tile below) before the [5:2] is played. Illustration 13 below shows some ways in which this configuration could develop.

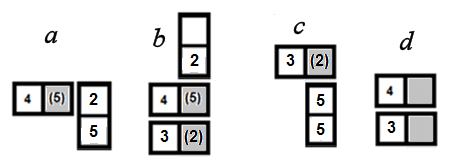
In cases a, b and c, further tiles can be added to build graphic A of illustration 12. In cases b and c the [5:2] can be added to score for a double figure combination. In case d the two adjacent blanks take on the value of zero, so the other tiles in image A of illustration 12 cannot be added.

Tactics

Game openings are likely to be cautious with players aiming to hinder each other’s attempts at scoring. But it is a game of chance as much as it is tactical and a player can only work with what is in hand and what they believe others are likely to play.

As the layout develops tiles will start to form patterns that can readily connect back to the main body of the Matrix.  In such cases a player is likely to be forced to place a tile that opens up chances for others to score. Being aware of what tiles have been used and those still awaiting play is crucial for success at this stage of the game.
Taking opportunities with “double figure combinations” is a good way of keeping a points tally ticking over. The thoughtful use of ‘double figure’ tiles is vital as placing a single ‘double numbered tile’ in open territory is likely to be punished.

Playing Matrix with different size sets:

The double six sets are adequate to provide two players with a challenging game of Matrix; double nine sets being ideal for games of longer duration or where three to four people play and double twelve sets being used where more than four play.

Playing Matrix with younger children:

For younger players it may be advisable to draw out a lined grid on paper or another material so that the tiles can be easily aligned when placed on the playing surface.